Quel rapport entre le jeu de la lumière dans un bol et le transport de tas de sable d’un point de la surface terrestre à un autre ? Des travaux modernes en transport optimal apportent un éclairage sur la question. Le problème du transport de masse remonte à Monge (1746-1818) et à son mémoire de 1784 « Sur la théorie des déblais et des remblais » : Monge y définit un coût de transport que l’on cherche à minimiser, d’où la notion d’optimalité. Le coût introduit par Monge est la somme – sur l’ensemble des particules à déplacer – du produit de la masse de chaque particule élémentaire par la distance qu’on lui fait parcourir. Dans le cas de la surface terrestre, pour un déblai éloigné du remblai, on peut penser que la forme de la Terre, plus particulièrement sa courbure, a une influence sur une éventuelle solution.
Les mathématiciens ont récemment montré l’existence et l’unicité d’une solution au problème de transport optimal sur une surface. La fonction de transport est ainsi bien définie ; à chaque point de la surface à déblayer elle assigne sa destination dans le remblai. Se pose alors la question de sa continuité : y a-t-il des « sauts » dans la position assignée quand on passe d’un point de la surface à un point infinitésimalement proche ? Il a en fait été démontré récemment que l’absence de telles discontinuités nécessitait qu’une condition liée à la géométrie de la surface sur laquelle on réalise le transport soit satisfaite.
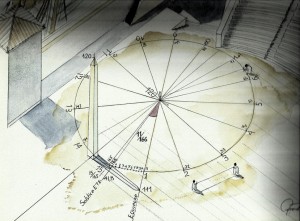
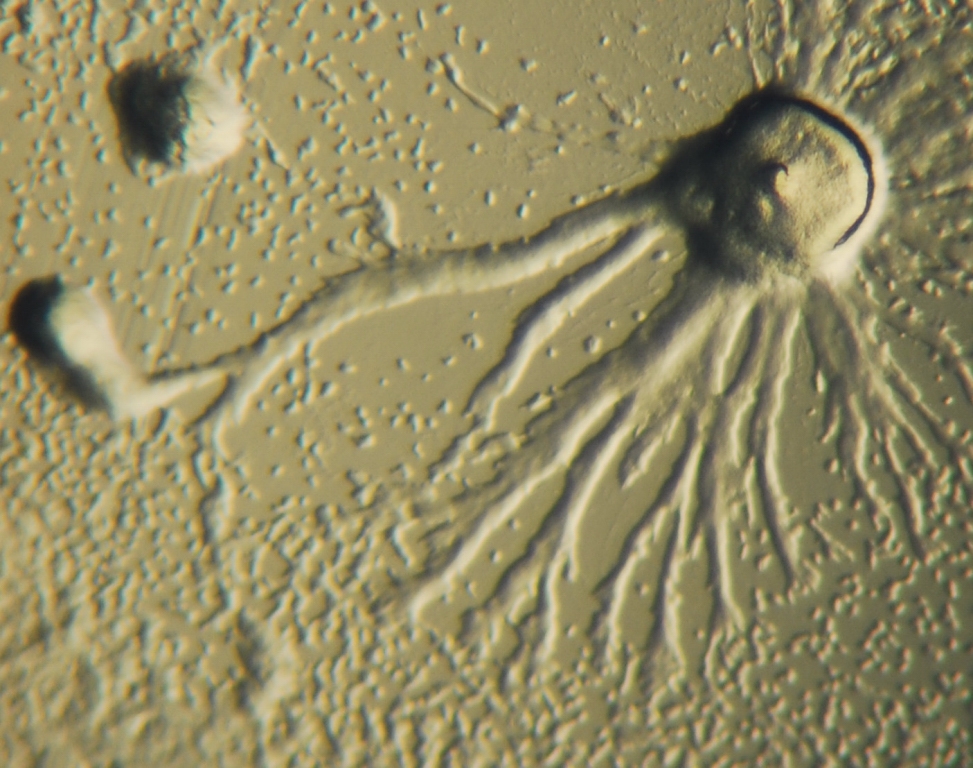
La Terre, que l’on peut assimiler à un ellipsoïde de révolution aplati, se situe entre deux cas limites : la sphère ou Terre ronde, pour laquelle le ratio entre le rayon polaire et le rayon équatorial vaut un, et le disque à deux faces ou Terre plate, pour laquelle ce ratio est nul. Pour la Terre ronde, la condition géométrique évoquée plus haut est satisfaite. Sur la Terre plate, partant d’un point du bord, suivre une ligne droite donne le plus court chemin, jusqu’à atteindre à nouveau le bord (on change ensuite de face, de sorte qu’il valait mieux suivre une corde sur l’autre face) ; on peut notamment en déduire que la condition géométrique n’est pas vérifiée sur la Terre plate. Le phénomène observé pour les rayons lumineux dans le bol correspond exactement au cas de la Terre plate : les rayons se réfléchissent sur le bord (ils changent de face !) pour se concentrer sur une courbe bien précise (une cardioïde) et former la figure lumineuse observée.
Concernant la condition géométrique nécessaire à la continuité du transport optimal, un calcul montre qu’il existe un seuil pour le ratio entre rayon polaire et rayon équatorial entre le cas de la Terre ronde, pour lequel la condition est satisfaite, et celui de la Terre plate pour lequel elle ne l’est pas. Sa valeur est (à peu près 0.577). Avec un ratio d’environ 0.996, la Terre (la vraie !) assimilée à un ellipsoïde de révolution ne présente donc pas d’obstruction à la continuité du transport optimal à sa surface.
Brève rédigée par Jean-Baptiste Caillau (Univ. Bourgogne) d’après les travaux de A. Figalli, L. Rifford et C. Villani et ceux de R. McCann.
Pour en savoir plus :
- Les brèves connexes « Géoïde, ellipsoïde et autres mots compliqués », « Querelle franco-anglaise autour de la forme de la Terre ».
- Y. Brenier (2012), La brouette de Monge ou le transport optimal, Images des mathématiques, CNRS.
- E. Ghys (2012), Gaspard Monge, le mémoire sur les déblais et les remblais, Images des mathématiques, CNRS
- Circle catacaustic, Wolfram mathworld.
Crédits Images : Wikimedia Commons.





2 Commentaires