Dessin de la méthode du calcul de l’obliquité de l’écliptique sur un gnomon.
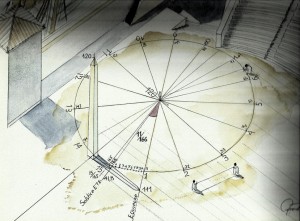
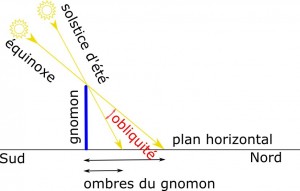
Pythéas est un navigateur et astronome marseillais qui vivait aux alentours de 300 av. J.-C. Il a fait un voyage célèbre jusqu’aux confins de l’Europe du Nord et réalisé plusieurs mesures astronomiques, dont celle de la latitude de Marseille. La plus remarquable de ces mesures sur le plan mathématique est celle de l’obliquité de l’écliptique, angle entre le plan de l’orbite terrestre et le plan de l’équateur. Cet angle est utilisé par les astronomes pour repérer le mouvement des étoiles et des planètes dans le ciel. Pour sa mesure, Pythéas utilise un gnomon, obélisque vertical dont il mesure l’ombre au solstice d’été et à l’équinoxe. L’angle entre les deux rayons est l’angle cherché.
La mesure verticale d’un angle étant délicate, il reporte la figure sur le sol afin de le faire plus facilement. L’angle est mesuré en fraction de circonférence, ce qui était courant à l’époque. L’angle est d’abord reporté 15 fois dans la circonférence et il y a un reste. Le reste est reporté 11 fois dans l’angle et il néglige le second reste. La circonférence vaut donc 15 x 11+1=166 fois le reste. En effet, si a désigne le rapport de l’angle à la circonférence, 1=15 a+r, a=11 r +r’. Pythéas décide que r’=0, cela donne a=11 r et 1=15 x 11 r + r=(15 x 11+1)r=166 r, puis r=1/166, a=11/166. Ce rapport correspond à un angle de (11/166) x 360°=23°51′, valeur légèrement supérieure à la valeur actuelle 23°27′ à cause des variations à long terme de l’inclinaison de l’axe de la Terre.
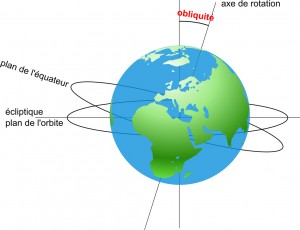
L’angle de l’obliquité de la Terre varie avec le changement à long terme de l’inclinaison de l’axe de la Terre.
Schéma explicatif de la mesure de l’obliquité de la Terre grâce à un gnomon.
L’écriture 11/166=1/(15+1/11) renvoie à ce qu’on désigne actuellement comme une fraction continue, théorie développée presque deux mille ans plus tard. L’idée est simplement d’approcher une fraction, ou un nombre réel plus petit que 1, en effectuant une suite de divisions euclidiennes donnant des quotients et des restes. Le procédé s’arrête au bout d’un nombre fini d’étapes si on part d’un nombre rationnel, mais il peut être poursuivi indéfiniment si on part d’un nombre irrationnel, d’où le nom de fraction continue.
C’est Christian Huygens, mathématicien et astronome hollandais, qui a été l’un des premiers à théoriser ces fractions continues au XVIIème siècle. On montre que ce procédé fournit les meilleures approximations fractionnaires d’un nombre réel donné, qu’on appelle les réduites de ce réel. Par exemple Pi admet 22/7 comme première réduite, valeur popularisée dans l’enseignement, et surtout 355/113 comme troisième réduite. Cette valeur est remarquablement précise, elle a 7 chiffres significatifs exacts et elle a été utilisée pendant des siècles comme valeur approchée de Pi, en particulier pour les calculs d’engrenages. Dans le cas de l’angle mesuré par Pythéas, 1/15 est la première réduite et 11/166 est la deuxième réduite.
Brève rédigée par Jean-Louis Maltret (IREM d’Aix-Marseille).
Pour en savoir plus :
- Hugues Journès, Yvon Georgelin, (2000), Aquarelles Jean-Marie Gassend. Pythéas. Éditions de la Nerthe.
- Thibaud Guyon, (2001), Pythéas l’explorateur. Archimède, l’école des loisirs.
- Claude Brezinski, (2005),Ces étranges fractions qui n’en finissent pas. IREM de la Réunion.
- François Herbaux, (2008), Puisque la Terre est ronde. Vuibert.
- (2013) Regards sur les mathématiques, itinéraires méditerranéens. Exposition de l’IREM d’Aix-Marseille.
Crédits images : Jean-Marie Gassend et Jean-Louis Maltret.
Imprimer
