Qu’il s’agisse de missions d’observation de la Terre, de ses océans, de son champ magnétique ou de télécommunications, l’utilisation de satellites en orbite autour de notre planète est devenue banale. Certains de ces engins spatiaux tirent parti de l’énergie solaire pour modifier leur trajectoire à l’aide d’une propulsion de très faible intensité. Le transfert de l’orbite de lancement vers l’orbite finale peut alors prendre plusieurs mois, et il convient d’optimiser la durée du transfert ou l’énergie consommée, entre autres critères.
On sait depuis Kepler (1571-1630) que pour des valeurs appropriées de position et vitesse, les orbites sont des ellipses. Une question naturelle est alors la suivante : étant donné deux orbites elliptiques parcourues dans le même sens, est-il possible de trouver une loi de commande du moteur du satellite lui permettant de réaliser le transfert de l’une vers l’autre ? La réponse à cette question de base de théorie du contrôle est positive, si petite soit la poussée dont dispose l’engin spatial. Parmi toutes les trajectoires réalisant le transfert, on peut alors chercher celles qui minimisent l’énergie nécessaire. Si l’on se donne un temps très long, on imagine qu’une poussée très faible suffira, mais qu’il faudra faire un grand nombre de révolutions autour de la Terre pour déformer continûment l’orbite initiale en l’orbite finale : une idée classique dans ce contexte consiste alors à ne regarder que l’évolution moyenne sur chaque tour des paramètres décrivant l’ellipse sur laquelle se trouve l’engin. Par un calcul explicite, T. N. Edelbaum, un ingénieur américain, a montré dans les années 60 que la détermination de ces trajectoires approchées revient pour l’essentiel à trouver les plus courts chemins sur une sphère déformée dont les deux coordonnées représentent l’excentricité (le caractère plus ou moins allongé de l’ellipse) et la position du périgée (point le plus proche de la Terre).
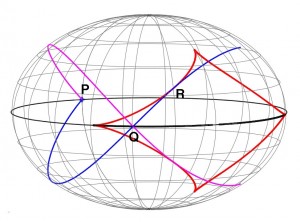
Surprise : la mesure des longueurs sur cette surface se fait presque comme sur un ellipsoïde de révolution aplati, de ratio rayon polaire / rayon équatorial égal à (environ 0.447 – nettement plus aplati que l’ellipsoïde de référence terrestre), ce qui éclaire la compréhension des transferts orbitaux à énergie minimale. Comme sur l’ellipsoïde de la figure, deux types de phénomènes se produisent lorsqu’on essaie de suivre un plus court chemin. Partant d’un point P à l’équateur (en noir sur la figure), suivons la courbe bleue : il s’agit bien d’une courbe de plus court chemin… jusqu’à ce qu’elle rencontre en Q (sur l’équateur) la courbe magenta symétrique. En outre, si on continue à suivre la courbe bleue au-delà de Q, celle-ci finit par toucher en R la courbe rouge en forme d’astroïde ; passé ce point de tangence, il existe pour aller vers les points visités depuis P des chemins plus courts que la courbe bleue et pourtant infinitésimalement proches de celle-ci. Notons que ce dernier phénomène ne se produit pas entre Q et R : une petite perturbation de la courbe bleue donne alors un chemin plus long.
La forme de la courbe rouge dépend du caractère plus ou moins aplati de l’ellipsoïde ; si on étire ce dernier pour qu’il s’approche d’une sphère, on verra l’astroïde se contracter jusqu’à devenir un seul point (symétrique du point P). Si au contraire on aplatit l’ellipsoïde au point d’obtenir un disque à deux faces, l’astroïde se déformera jusqu’à donner la cardioïde dans le bol de la brève précédente.
Brève rédigée par Jean-Baptiste Caillau (Univ. Bourgogne).
Pour en savoir plus :
- La brève connexe Tout autour de la Terre.
- SWARM – Mieux comprendre le fonctionnement de la Terre.
- Moteur ionique.
- Garder le contrôle… à l’aide des mathématiques, K. Beauchard, J.-M. Coron et P. Rouchon.
Crédits images : Wikimedia Commons.




1 commentaire