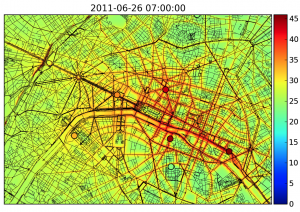
Carte de pollution en dioxyde d’azote (en μg/m3).
Les disques colorés sont les stations de mesure Airparif.
L’air que nous respirons contient de nombreux polluants. Les activités humaines sont naturellement en cause : trafic automobile, émissions industrielles, agriculture, etc. Mais la nature produit également des polluants tels que les Composés Organiques Volatils émis par la végétation et les poussières des éruptions volcaniques.
Il est important d’étudier l’exposition des populations à la pollution afin de comprendre les conséquences sur la santé et de prendre les mesures réglementaires nécessaires. Depuis octobre 2013, l’Organisation Mondiale de la Santé classe la pollution de l’air extérieur parmi les causes de groupe I dans les décès par cancer. La démonstration de causalité est très difficile à valider hors du contexte accidentel, puisque les personnes sont généralement soumises à des concentrations relativement faibles, mais sur de longues périodes. Les méthodes épidémiologiques classiques, qui comparent un groupe d’individus exposés au phénomène à un groupe témoin, ne sont pas utilisables.
Des mesures de concentration de polluants sont disponibles grâce à des capteurs dédiés. Ces mesures sont complétées, sur le reste du territoire par un modèle numérique de qualité de l’air. Ce modèle traduit le mécanisme de transport des polluants dans l’atmosphère et les réactions chimiques qui se produisent entre ces polluants. Il prend également en compte la disparition de polluants en raison des pluies et du dépôt sur le sol. Afin de fournir des prévisions performantes et de permettre aux décideurs de prendre des mesures adaptées en cas de risque sur la santé, le modèle nécessite de nombreuses données d’entrée, telles que la direction et la force des vents, les nuages, etc. Celles-ci sont souvent connues de façon approximative. C’est également le cas des valeurs des paramètres utilisés par le modèle numérique. En raison de ces approximations, les prévisions de qualité de l’air sont entachées d’une incertitude.
Connaître l’incertitude d’une prévision est crucial pour analyser objectivement les risques encourus par la population et prendre des décisions optimales. Pour ce faire, il est possible de considérer un ensemble de simulations, effectuées par le modèle en prenant différentes valeurs des données d’entrée et des paramètres. La méthode de Monte-Carlo nous dit (sous certaines hypothèses mathématiques) que la moyenne de ces simulations est une bonne approximation de la prévision optimale. De plus, la dispersion de l’ensemble (autrement dit l’accord ou le désaccord entre les membres de l’ensemble) nous renseigne sur l’incertitude associée à la prévision.
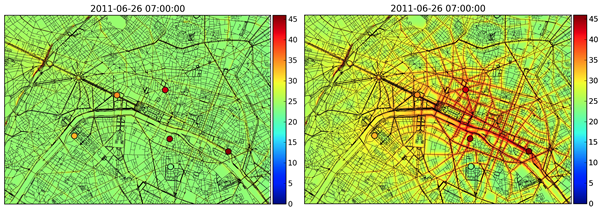
Simulation seule (gauche), simulation et assimilation des données mesurées (droite).
Projet Votre Air : collaboration Airparif, Inria, Numtech
Les mesures de concentration de polluants sont les observations de la réalité qui sont disponibles pour améliorer les résultats des modèles et les rendre plus proches de la réalité. Ces observations peuvent être utilisées de plusieurs façons, dans un cadre mathématique qui s’appelle l’assimilation de données. Une prévision optimale peut, par exemple, être calculée grâce à la moyenne pondérée de résultats issus d’un ensemble de modèles, auxquels on donne plus ou moins de poids en fonction des mesures passées. La prévision peut également être effectuée en utilisant simultanément les résultats du modèle et les observations, tout en prenant en compte la confiance accordée à chacun.
Brève rédigée par Isabelle Herlin et Vivien Mallet (équipe Clime du centre Inria Paris-Rocquencourt).
En savoir plus :
- Interview (podcast) de Vivien Mallet sur le site Interstices.
- Pollution atmosphérique. Des processus à la modélisation. (Livre de Bruno Sportisse)
- Projet Votre Air : Collaboration Airparif, Inria, Numtech.
- Brève connexe : Prévoir les crues : avec quelle (in)certitude?
- Brève connexe : Où vont les nuages?
Crédits images : Inria, équipe CLIME.




2 Commentaires