Le fragment principal de la machine. Taille d’environ 20 cm par 20 cm.
Lors d’une visite des réserves du Musée National Archéologique d’Athènes, en 1902, le mathématicien Spyridon Staïs cherchait des fragments d’une magnifique statue, l’éphèbe, récupérée avec des centaines d’autres objets dans l’épave d’un navire romain près des côtes de l’île d’Anticythère. Parmi ces fragments, Spyridon Staïs remarqua des bouts de roues dentées sur lesquels de toutes petites inscriptions apparaissaient sous les calcifications des sédiments marins.
Très vite, les spécialistes s’accordèrent sur la nature de l’objet : il s’agissait des restes d’une machine astronomique. Alors commença une dispute qui devait durer presque un siècle : était-ce un astrolabe, un planétarium, un instrument de navigation ou bien encore autre chose ? Les indices pour résoudre l’énigme étaient épars : trois dizaines de roues dentées visibles sur des radiographies et quelques centaines de caractères gravés en grec ancien sur les fragments de bronze et lisibles à l’œil nu.
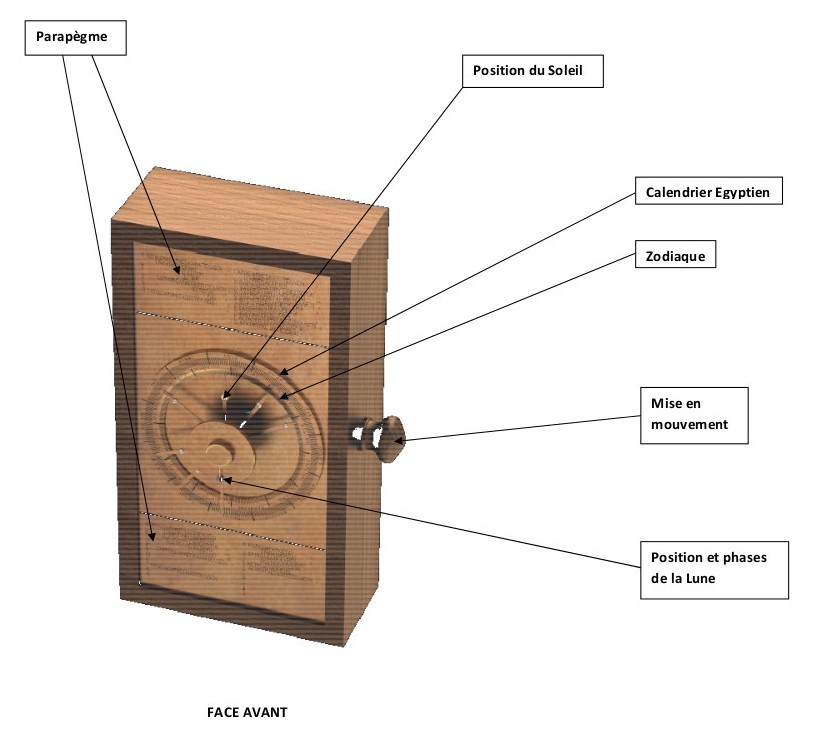
Reconstruction d’une machine d’Anticythère : vue de face.
Parmi ces indices, deux nombres : 19 et 76, déchiffrables parmi des termes astronomiques et mécaniques. Les spécialistes de l’astronomie antique les avaient tout de suite reconnus comme correspondant à la durée en années des cycles lunisolaires de Méton et de Callippe. Un cycle lunisolaire est un commun multiple (approximatif) d’une année solaire et d’un mois lunaire : au bout de 235 mois lunaires (nombre également gravé sur la machine), il s’est écoulé 19 ans et à peine plus d’une heure et demie. Le cycle de Callippe est une approximation différente (et meilleure).
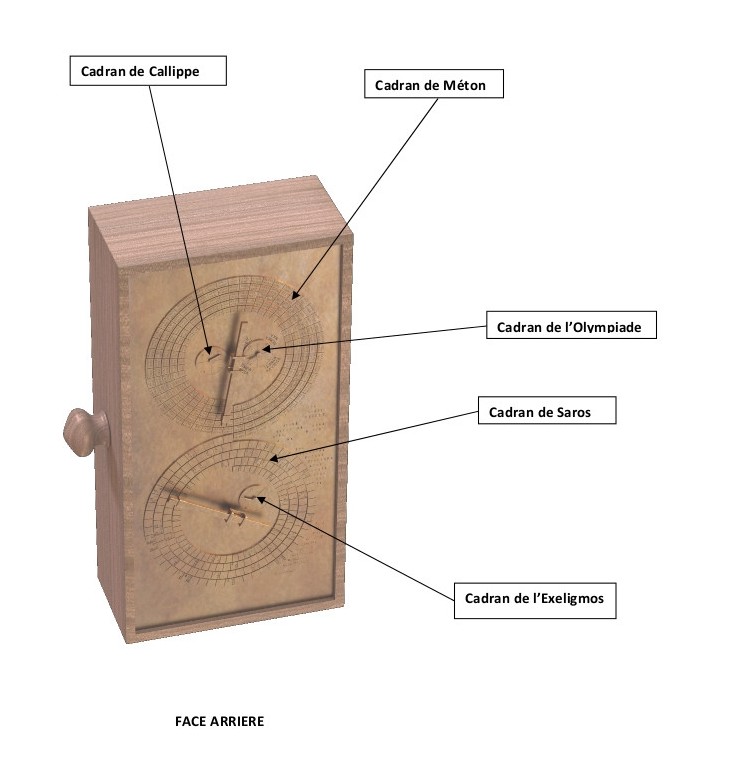
Vue de dos.
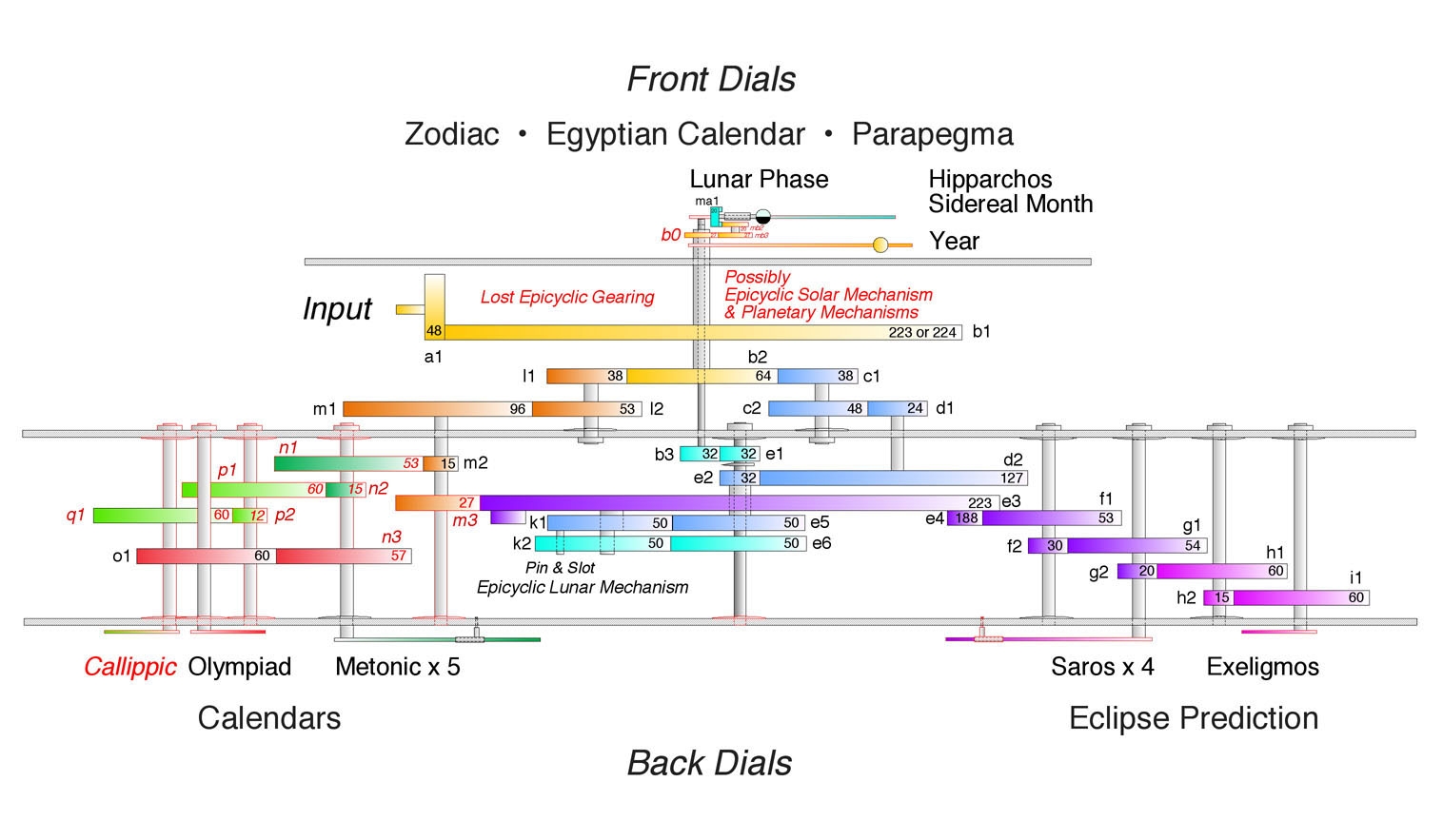
En choisissant une date sur le calendrier solaire égyptien, l’utilisateur de la machine peut voir sur la face avant les positions et les phases de la Lune ainsi que les positions du Soleil et des cinq planètes connues à l’antiquité. Sur la face arrière sont notamment indiqués les mois lunaires du calendrier civil dans les cycles de Méton et Callipe. Raffinement de la science du second siècle avant notre ère, le mouvement apparemment irrégulier de la Lune est aussi calculé, avec les ralentissements et accélérations dus à la forme elliptique de son orbite.
Mais comment est-ce possible ? Grâce à un système complexe de roues dentées.
Diagramme possible du système de roues dentées.
Un bouton (ou une manivelle) fait tourner tous les rouages d’une manière solidaire. Quand on fait tourner un axe sur lequel sont fixées deux roues dentées ayant respectivement N et M dents, un tour complet de la roue à N dents fait faire avancer de M dents la seconde roue. Ainsi, une dent de la première fait avancer M/N dents de la seconde. Si cette seconde roue en entraîne une troisième d’un autre axe à deux roues, qui ont respectivement Q et P dents, avancer une dent de la première roue fera avancer la quatrième roue de (M/N)(P/Q) dents. Et ainsi de suite. Par exemple, pour le mois lunaire sidéral, le rapport voulu est de 254/19 (254 mois synodiques pour 19 ans). Or, le nombre de dents du train d’engrenages impliqué est : (64/38)(48/24)(127/32), ce qui est égal à (2×32/2×19)(2×24/24)(127/32) = (2×127/19) = 254/19 !
Les férus de mathématiques et d’astronomie peuvent dès à présent chercher les bons rapports pour les trains d’engrenages entraînant les aiguilles des planètes : en effet, cette partie de la machine étant probablement encore au fond de la mer d’Anticythère, il n’y a pas de consensus des spécialistes sur la façon de reproduire les mouvements des planètes. A vos calculettes donc !
Brève rédigée par Yanis Bitsakis (Université d’Athènes, Programme d’histoire, philosophie et didactique des sciences et des techniques).
Pour en savoir plus :
- La vidéo des expositions « Anticythère ».
- La bibliographie du site de l’équipe de recherche sur la machine d’Anticythère.
Crédits Images : Wikimedia Commons, Hublot, Genève. Police “Anticythère” : Université Aristote de Thessalonique, Tony Freeth et Antikythera Mechanism Research Project.
Imprimer
