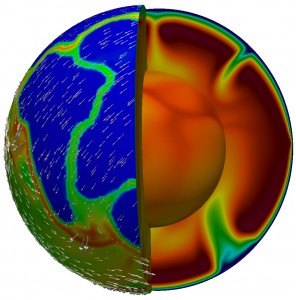
Modèle numérique de convection thermique du manteau terrestre. La couleur en surface représente la résistance des roches : bleu pour les roches résistantes (continents) et rouge pour les roches peu résistantes (limites entre les plaques, chaînes de montagnes). Les flèches indiquent la vitesse en surface calculée. La couleur en profondeur représente la température : bleu pour les zones froides, rouge pour les zones chaudes.
La Terre est en mouvement : les continents dérivent et les fonds marins sont en expansion. Autour de l’Océan Pacifique notamment, les roches du plancher océanique s’enfoncent sous l’effet de leur poids dans les profondeurs du manteau terrestre. Ces lents déplacements (de quelques centimètres par an) sont rendus possibles par la plasticité des roches qui composent les couches profondes de la Terre. Ils permettent à notre planète d’évacuer son trop-plein d’énergie interne à la manière d’un moteur. C’est le phénomène de convection thermique, qui s’exprime à la surface du globe par la tectonique des plaques.
La tectonique des plaques est une théorie née à la fin des années 1960, qui décrit les cent premiers kilomètres de la Terre solide comme un puzzle de couches minces et rigides se déplaçant les unes par rapport aux autres. Cette hypothèse a ouvert une porte de la géologie aux mathématiques. En effet, l’hypothèse de plaque rigide permet de décrire et reconstruire le déplacement de la surface terrestre grâce aux outils de géométrie sur la sphère. Ce cadre mathématique donne les moyens d’estimer la vitesse de déplacement en tout point du globe. Les vitesses prédites sont en très bon accord avec les mesures de vitesses instantanées, réalisées notamment grâce au GPS sur les continents. Cependant, la tectonique des plaques demeure un instrument de description limité à la surface de la Terre qui ne peut estimer les forces à l’origine des mouvements. Cette théorie ignore la déformation observée dans les chaînes de montagnes, les plaques étant supposées parfaitement rigides. Au total, près de 20% de la surface du globe ne peuvent être décrits par des plaques indéformables.
La convection thermique est une théorie plus complète qui relie les déplacements de surface aux mouvements profonds à leur origine, en prenant en compte la déformation des roches. Cette déformation dépend d’un comportement mécanique des roches qui n’est pas du tout linéaire, ce qui rend difficile l’approximation numérique des équations aux dérivées partielles concernées. Trente ans ont été nécessaires aux géophysiciens pour mettre en œuvre des méthodes développées en analyse numérique et des algorithmes performants pour obtenir des solutions numériques aux équations de la convection du manteau dans un régime réaliste. Grâce à des méthodes mathématiques en progrès constant et à l’augmentation de nos capacités de calcul, on peut dorénavant envisager de dépasser la tectonique des plaques et d’établir les liens entre la tectonique de surface et les lents mouvements profonds du globe.
Brève rédigée par Nicolas Coltice (Laboratoire de Géologie de Lyon, Université Lyon 1) et Alexandre Fournier (Institut de Physique du Globe de Paris), d’après ses propres travaux et ceux de Tobias Rolf, et Paul Tackley.
Pour en savoir plus :
- Conférence de Nicolas Coltice “La grande saga des continents : quel avenir pour la tectonique des plaques ?” http://youtu.be/Mwa_-WZKNFU
- Article de vulgarisation sur la convection mantellique : http://planet-terre.ens-lyon.fr/article/convection-mantellique-tectonique-plaques.xml
Crédits images : Léa Bello et Nicolas Coltice.







1 commentaire