
Les Eléments d’Euclide. Un des plus anciens diagrammes existants. Fragment de papyrus trouvé sur la rive ouest du Nil.
Comment comparer entre elles deux surfaces rectilignes de formes différentes ? Hérodote attribuait à ce problème l’origine de la géométrie. Qu’en est-il pour les rectangles ? Les rectangles peuvent avoir des formats très différents et il n’est pas facile d’en comparer géométriquement les surfaces.
Le problème serait résolu si on pouvait transformer chaque rectangle en un carré car tous les carrés ont la même forme et peuvent donc être superposés.
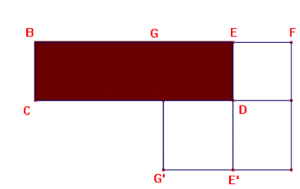
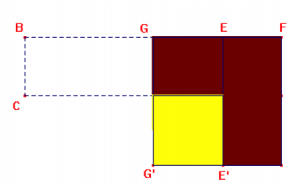
Mais comment faire pour transformer géométriquement un rectangle donné, BCDE, en un carré de même aire ?
Voici les étapes de la solution, données sous forme de bande dessinée :
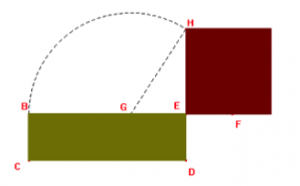
Il faut tout d’abord adjoindre les deux côtés, ici [BE] et [ED], puis construire le milieu G du segment [BF] obtenu.
On s’aperçoit alors que l’aire du rectangle est égale à celle du carré construit sur [GF], privée de celle du petit carré jaune.
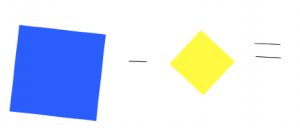
Notre problème se réduit alors au suivant : comment construire un carré égal en aire à la différence de deux carrés donnés ?
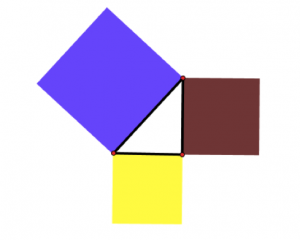
La solution, tout le monde la connaît, mais souvent sans vraiment bien la connaître. Il suffit de construire un angle droit : c’est le théorème dit de Pythagore !
De ce point de vue, les droites perpendiculaires du théorème de Pythagore constituent la configuration abstraite qui permet de résoudre le problème très concret de l’origine de la géométrie selon Hérodote : ramener toute figure rectiligne à un carré de même aire, c’est-à-dire en réaliser la quadrature.
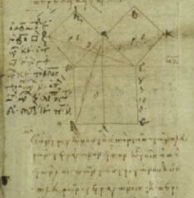
Les Éléménts, livre I, proposition 47 : le théorème dit de Pythagore. Extrait d’un des plus anciens manuscrits complets conservés.
Les quadratures ont joué un rôle important dans le développement de la géométrie. Elles illustrent bien ce que les Grecs de l’antiquité appelaient un problème. De quoi s’agit-il ? Dans le cadre des joutes oratoires qui étaient monnaie courante dans le monde grec et contrairement au principe des cours magistraux d’aujourd’hui, c’était le public qui exhortait l’orateur à s’exprimer sur un sujet en lançant à ce dernier un problème. Dans l’idée de problème entre ainsi l’idée de quelque chose qu’on se propose de faire mais dont ne voit pas à l’avance à quelle conclusion on peut aboutir et comment. Un grand problème demande ainsi que l’on invente une voie pour le résoudre et peut par conséquent affecter la manière dont les mathématiques évoluent. Sa résolution peut supposer de longues recherches, une patiente accumulation de résultats intermédiaires qui, dans le cas de la quadrature des figures rectilignes, constituent bon nombre de propositions des Eléments d’Euclide. Plutôt que de le résoudre d’un coup, il est souvent nécessaire de chercher à le déplacer ou bien de le réduire en tournant autour, parfois pendant plusieurs millénaires comme dans le cas du célèbre problème de la quadrature du cercle.
Brève rédigée par Frédéric Brechenmacher, Université d’Artois & École polytechnique.
Pour en savoir plus :
- B. Vitrac, “L’origine de la géométrie grecque” et “Le cas Hippocrate”, Culture MATH.
- C. Goldstein. (1989), L’un est l’autre. Pour une histoire du cercle, in M. Serres (ed.), Eléments d’histoire des sciences, Larousse, Paris.
- A. Bernard, Ancient rhetoric and Greek mathematics : a response to a modern historiographical dilemma, Science in Context, 16(3), pp. 391-412.
- Brève reliée : Carrer la Terre, une origine de la géométrie.
Crédits images : University Museum, University of Pennsylvania, Philadelphia, USA. Bibliothèque du Vatican.






Même avec des pieds d’argile, Pythagore a bien compris que les principes de la géométrie proviennent du ciel.
Le 22 novembre 2013