Carrer la Terre : une origine de la géométrie

Egyptiens travaillant dans les champs.
On aperçoit la borne blanche délimitant le domaine. A gauche: l’inspecteur chargé de la collecte des taxes. Les hiéroglyphes indiquent : comme le grand dieu dans les cieux juge la position de la pierre correcte, sa position est solide.

Geo: terre. Metron: mesure. D’où vient la géométrie ? Il y a plus de 2400 ans, Hérodote en attribuait l’invention aux problèmes posés par les crues du Nil en ancienne Égypte : « Ce roi (Sésostris d’Egypte) partagea le sol entre tous les Egyptiens, attribuant à chacun un lot égal aux autres, carré, et c’est d’après cette répartition qu’il établit ses revenus, prescrivant qu’on payât une redevance annuelle. S’il arrivait que le fleuve (le Nil) enlevât à quelqu’un une partie de son lot […], lui, envoyait des gens pour mesurer de combien le terrain était amoindri afin qu’il fût fait […] une diminution dans le paiement de la redevance. […]. C’est ce qui donna lieu, à mon avis, à l’invention de la géométrie, que les Grecs rapportèrent dans leur pays.»

Comment interpréter l’attribution à chaque Égyptien d’un lot carré ? Les berges du Nil ne sont pas un damier à la New-yorkaise. On pourrait, bien entendu, voir ici une allusion au choix d’une unité, comme notre “mètre-carré”, afin d’associer à toute aire un nombre : sa mesure. Mais une autre interprétation est, non seulement possible, mais aussi plus séduisante, au sens où elle ne fait appel qu’à des procédures purement géométriques : les procédures de quadratures.

Comparer des surfaces qui n’ont pas la même forme n’est pas évident.

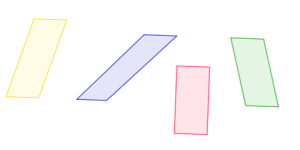
Il s’agit là d’un problème très concret : comparer entre elles des surfaces. Or, cela est loin d’être évident lorsque ces surfaces n’ont pas la même forme. Par exemple, comment déterminer quels sont les parallélogrammes ci-contre qui ont la même aire sans utiliser de nombre? Parmi les propriétaires de tels champs, lesquels devront payer le même impôt ? Répondre au problème d’Hérodote nécessite de savoir manipuler des formes sans en modifier la surface.

Des objets abstraits pour simplifier le calcul.

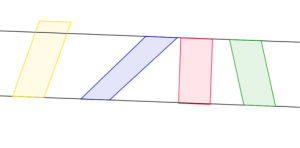
On peut remarquer ici que tous ces parallélogrammes ont un côté superposable, donc de même longueur. Par ailleurs, trois d’entre eux peuvent être placés entre deux droites parallèles : ils ont pour cette raison la même aire, que l’on peut d’ailleurs visualiser comme égale à celle du rectangle rouge.

Ainsi, pour résoudre un problème concret sur des surfaces, nous avons fait appel à des objets abstraits : des droites parallèles. De ce point de vue, la géométrie tire son origine d’une formalisation de pratiques humaines comme les techniques d’arpentage.

Détail de “L’École d’Athènes”, fresque de Raphaël.

Les Éléments d’Euclide, célèbres pour leur structure axiomatique,  portent encore la marque de ces savoirs pratiques. La proposition 36 du livre I, celle dont nous nous sommes servis plus haut, y est ainsi formulée : «Les parallélogrammes  qui sont sur des bases égales et dans les mêmes parallèles sont égaux entre eux». Comme tout parallélogramme est composé de deux triangles égaux, on peut alors démontrer la proposition 37 : « Les triangles qui sont sur la même base et dans les mêmes parallèles sont égaux entre eux ». 

Avec ces deux résultats, il est facile de transformer n’importe quel triangle en un rectangle de même aire : il suffit de tracer des parallèles. Or, ce résultat est crucial: toute figure rectiligne est décomposable en triangles et peut donc être  transformée en un rectangle de même aire en utilisant uniquement une règle non graduée et un compas.

Le problème d’Hérodote se réduit ainsi finalement à comparer entre eux des rectangles. Comment s’y prendre ? Rendez-vous dans une prochaine brève.

Brève rédigée par Frédéric Brechenmacher, (Université d’Artois & École polytechnique).

Pour en savoir plus :

• J.Ritter (1989), Chacun sa vérité : les mathématiques en Égypte et en Mésopotamie, in M. Serres (ed.), Eléments d’histoire des sciences, Larousse, Paris.
• E.Giusti (2000), La naissance des objets mathématiques, Ellipses, Paris.
• Brève reliée : Pythagore aux pieds d’argile.

Crédits images : British Museum, Palais du Vatican.

Imprimer