Des codes correcteurs d'erreurs pour les télécommunications

Les communications sans fil dans l’ère du monde.

Les télécommunications sont devenues indispensables dans notre vie quotidienne. Cet échange numérique d’informations se fait par le biais de canaux de communication comme le câble, la fibre optique, le Wifi, les satellites, etc. Ces canaux ne sont pas tous fiables à 100%, ils sont soumis à des perturbations qui peuvent altérer l’information qui les traverse. Pour résoudre ce problème, on utilise des codes correcteurs d’erreurs.

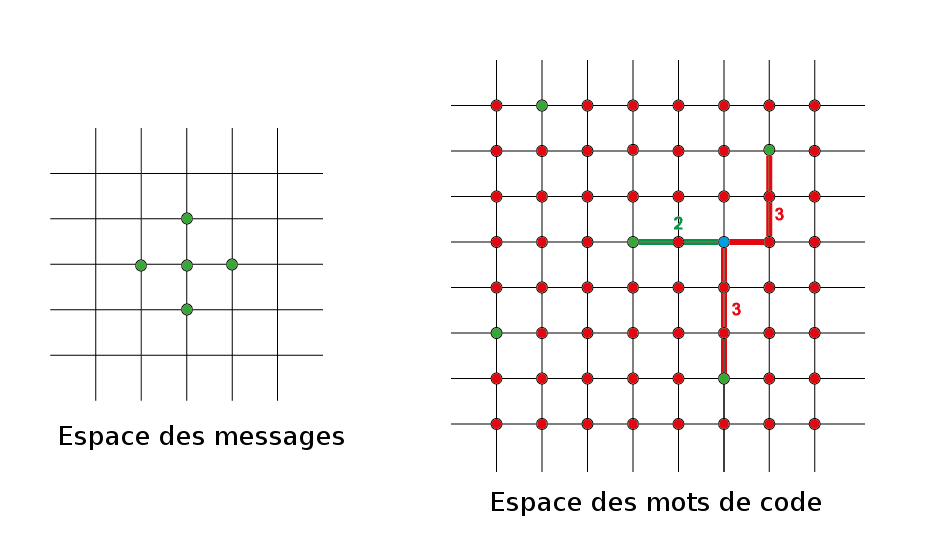
Le principe est simple, l’expéditeur va enrichir le message et le transformer en ce que l’on appelle un mot de code. Un message est une suite de symboles. Un mot de code est le message auquel on a ajouté des symboles qui doivent permettre de corriger les erreurs qui pourraient survenir lors de la transmission. C’est ce que l’on appelle la redondance. Dans l’exemple ci-dessous, les messages originels sont représentés par les points verts dans la partie gauche du schéma, et les mots de code correspondants (les messages ainsi encodés) sont représentés par les points verts dans la partie droite du schéma. Ces derniers sont plongés dans un ensemble plus grand de mots de code, dans lequel les points rouges ne sont pas des mots de code issus de l’encodage d’un véritable message. Cela revient à avoir dans ce nouvel ensemble de points un dictionnaire des mots autorisés, ici désignés par les points verts. Ainsi, lorsque le destinataire reçoit un mot (le point bleu sur le schéma de droite), il vérifie s’il appartient au dictionnaire et si ce n’est pas le cas, il suppose qu’il y a eu un nombre d’erreurs minimal et il choisit le mot de code autorisé le plus proche du mot de code erroné dans l’espace des mots de codes. Dans l’exemple du schéma, il choisit le point vert du milieu car il n’est qu’à distance 2 alors que les autres sont au moins à distance 3.

Il existe beaucoup de codes correcteurs différents selon les mathématiques sur lesquelles ils sont construits. Le code le plus simple est le code de répétition. Si le message à envoyer est 1 alors on encode en 111 et si c’est 0 alors on encode en 000. Ainsi, s’il y a une erreur, on reçoit par exemple 100, et on prend alors le mot de code autorisé le plus proche, c’est-à-dire 000. Cependant, si on envoie 000 et qu’il se produit 2 erreurs pendant la transmission, on va alors recevoir 110 et on va corriger en 111, ce qui n’est pas le mot de code envoyé. Ce code ne peut donc corriger qu’une seule erreur. Mais il est gourmand en symboles ajoutés puisque, pour un message d’un symbole, il rajoute 2 symboles. Le débit est donc divisé par 3.

Des codes correcteurs utilisant des mathématiques plus avancées, comme les codes convolutifs, les codes LDPC, les codes de Reed-Solomon, les codes de Goppa, etc, permettent d’obtenir de meilleures performances en termes de correction et de débit. Cependant, la multiplication des échanges numériques et l’envoi de messages de plus en plus volumineux demandent un débit toujours plus rapide. Trouver des codes correcteurs encore plus performants est donc une nécessité et les mathématiques jouent un grand rôle dans cette recherche.

Brève rédigée par Marion Candau (LMBA, Univ. de Bretagne Occidentale).

Pour en savoir plus :