Modèle proie-prédateur | Mathématicien Vito Volterra

A l’origine du modèle appelé « proie-prédateur » il y a un grand mathématicien italien, Vito Volterra (1860-1940) et une histoire de poissons.

Pendant la première guerre mondiale, Volterra fut très engagé comme militaire (malgré son âge) et comme directeur de « l’Ufficio Invenzioni e Ricerche ». Il fut l’un des mathématiciens italiens les plus actifs d’un point de vue scientifique et institutionnel : pendant les années 20, il fonda le « Consiglio Nazionale delle Ricerche » (CNR) (l’équivalent du CNRS français) avec la conviction que les mathématiques étaient de plus en plus indispensables aux autres sciences.

Dans une série de leçons données à l’Institut Henri Poincaré à Paris en 1928-29 (Leçons sur la théorie mathématique de la lutte pour la vie), Volterra rappelle les raisons qui l’ont amené à s’occuper de l’interaction entre les formes biologiques qui vivent dans un même écosystème : « A la suite de conversations avec monsieur D’Ancona, qui me demandait s’il était possible de trouver quelque voie mathématique pour étudier les variations dans la composition des associations biologiques, j’ai commencé mes recherches sur ce sujet à la fin de 1925. » Le biologiste Umberto D’Ancona (1896-1964) était le beau-fils de Volterra et sa question, à la fois scientifique et commerciale, était très simple : comment interpréter certaines statistiques qui montraient la fluctuation des poissons de la mer Adriatique en relation avec l’activité de pêche.

L’idée géniale de Volterra fut de distinguer les habitants de la mer en deux grandes catégories : les proies et les prédateurs, deux quantités variables en fonction du temps. En introduisant des hypothèses simplificatrices, Volterra trouva une formule qui lie la variation des proies à celle des prédateurs. Cette équation dépend de plusieurs facteurs, par exemple les taux de natalité et mortalité, ou encore le nombre initial d’individus des deux populations.

Evolution des populations de proies et de prédateurs au cours du temps

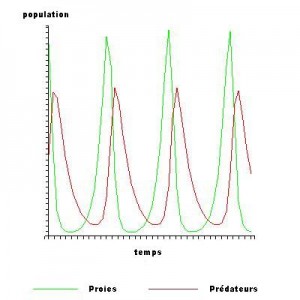
Cette relation mathématique admet l’interprétation biologique suivante (visible sur la figure) : si au début on suppose que les deux populations – les proies et les prédateurs – sont en nombre très faible, alors les proies tendent à se multiplier assez vite car les rencontres proies-prédateurs sont très rares. Quand le nombre de proies augmente, les prédateurs trouvent plus de nourriture. Leur nombre croit plus rapidement qu’avant. Par conséquence, les proies diminuent et les rencontres entre prédateurs et proies se raréfient. Le nombre de prédateurs commence alors à diminuer à cause du manque de nourriture et par conséquence le nombre de proies augmente, et ainsi de suite. Ce modèle, connu sous le nom de Lotka-Volterra, est l’un des premiers exemples de dynamique des populations, un domaine de recherche de plus en plus actif qui aujourd’hui développe des modèles beaucoup plus compliqués.

Brève rédigée par Rossana Tazzioli (Univ. Lille 1) d’après les travaux de Vito Volterra, Leçons sur la théorie mathématique de la lutte pour la vie, Paris, Gauthier-Villars, 1931 (réimpr. Jacques Gabay en 1990).

Pour en savoir plus :

Crédits Images: Fig 1) Dreamstime, Fig 2) Wikipedia.

Imprimer