John Forbes Nash, Jr.
John Forbes Nash Jr est né en 1928 à Bluefield aux États-Unis, en Virginie-Occidentale. Poussé par ses enseignants sur la voie des mathématiques, il prépare une thèse à l’université de Princeton. Durant ces années, il a inventé le jeu de hex pour la salle commune des élèves et des professeurs. John Nash s’intéresse à la fois à la théorie des jeux et à des problèmes de géométrie ou de topologie. Comme beaucoup d’autres (par exemple Richard Bellman), il va travailler à la RAND corporation, qui, dans un contexte de guerre froide, s’intéresse beaucoup à la théorie des jeux. De santé mentale fragile, il est happé par sa schizophrénie à la fin des années 1950 et ne refera surface que dans les années 1990.
Pour expliquer la notion d’équilibre introduite par Nash dans son mémoire de thèse, observons Paul et Carole jouer de façon rationnelle de la façon suivante : dans les tableaux ci-dessous, Paul choisit la ligne (haute H ou basse B) et Carole, elle, choisit la colonne (gauche G ou droite D). Le chiffre qui apparaît dans la case ainsi choisie désigne ce que gagne Paul et ce que perd Carole. Ainsi, si c’est un nombre négatif, c’est Carole qui gagne et Paul qui perd.
Trois exemples de jeu à deux joueurs et deux stratégies par joueur.
Dans le premier jeu de la figure ci-dessus, on voit que Paul a intérêt à choisir la ligne du haut : en effet, que Carole choisisse G ou D, Paul gagne plus avec H qu’avec B. On dit que choisir H est une stratégie dominante pour Paul. Observez que G est une stratégie dominante pour Carole : elle gagne plus avec G qu’avec D, quel que soit le choix de Paul. Ainsi, (H,G) est un équilibre en stratégies dominantes. Dans le second jeu, c’est Carole qui a une stratégie dominante, G. Paul n’en a pas : si Carole choisit G, alors Paul doit choisir B, mais si Carole choisit D, alors il doit choisir H. Quoi qu’il en soit, le choix (B,G) est un équilibre de Nash : si un des joueurs modifie sa stratégie unilatéralement, c’est-à-dire sans que l’autre ne change la sienne, il n’augmente pas son gain. Dans le troisième jeu, il n’y a pas d’équilibre de Nash : s’il y en avait un, ce serait forcément (B,G) ou (H,D) pour Paul alors que ce ne pourrait être que (H,G) ou (B,D) pour Carole.
La notion d’équilibre qu’a inventée Nash s’applique aujourd’hui dans des domaines variés, tels que l’économie, les sciences politiques, la sociologie ou la biologie. John Nash a reçu pour cela (avec John C. Harsanyi et Reinhard Selten) le prix Nobel d’économie en 1994.
Brève rédigée par Cyril Imbert (CNRS et Univ. Paris-Est Créteil) d’après les travaux de John Nash (Princeton University), J. J. O’Connor; E. F. Robertson (University of St Andrews).
Pour en savoir plus :
- Vidéo de la conférence de C. Villani (2010), « Les prodigieux théorèmes de Monsieur Nash », dans le cadre du cycle Un texte, un mathématicien.
- J. J. O’Connor; E. F. Robertson (2002), « John Forbes Nash, Jr. », MacTutor History of Mathematics archive, University of St Andrews.
- La page wikipedia sur la Théorie des jeux.
- Brèves connexes : « Paysages urbains équilibrés », « Propriétés émergentes en économie », « Créer de nouvelles routes peut générer davantage
d’embouteillages ». - Frédéric Le Roux (2012), « Le jeu de hex », Images des mathématiques, CNRS.
Crédits Images : Wikimedia commons.
Imprimer
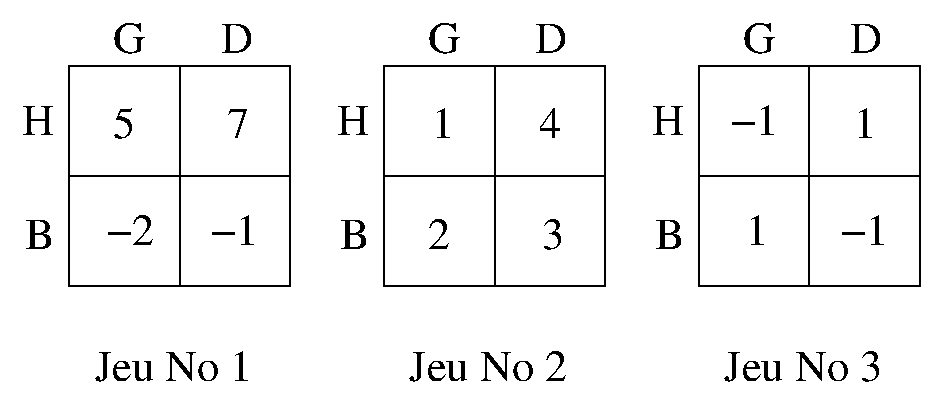
ce qui est troublant c’est le jeu numéro deux, car Carole a une stratégie dominante alors qu’elle ne gagne rien, et c’est Paul qui l’emporte à tous les coups, par contre elle devient stratégie dominante du fait même qu’elle ne gagne rien et qu’elle peut influencer le nombre de points que remporte Paul. Ce qui le rend dépendant d’elle quand bien même il gagne à tous les coups…et qu’elle n’a rien à perdre.