Portrait de Newton.
Depuis Newton, on sait que la Terre exerce une force d’attraction sur une pomme tombant de son arbre et sur tout autre objet de masse non nulle. C’est ce qu’on appelle la force de gravitation. De plus, comme la Terre tourne, la force centrifuge vient s’ajouter à la force de gravitation pour donner la force de pesanteur. Afin de connaître la valeur de cette force pour n’importe quel objet situé à n’importe quelle hauteur, il suffit de déterminer le potentiel terrestre : c’est une fonction de la position de l’objet, qui dépend de la forme et de la masse de la Terre. La connaissance du potentiel terrestre est essentielle pour calculer la trajectoire d’un satellite ou pour définir précisément la notion d’altitude, pour les montagnes et les avions par exemple.
Le niveau moyen des mers, représenté par le géoïde terrestre, définit l’altitude zéro à partir de laquelle sont mesurées les altitudes. Le géoïde est tel qu’en tous ses points, le potentiel de pesanteur est le même. Il est déterminé dès que l’on sait calculer le potentiel terrestre. Mathématiquement, la Terre est relativement bien représentée par un ellipsoïde avec une densité de masse homogène. Si la Terre était exactement cet ellipsoïde, le géoïde serait tout simplement la surface géométrique. Mais la Terre n’est pas un ellipsoïde homogène, donc le niveau moyen des mers n’est pas aussi régulier que l’on pourrait le penser !
Il est donc nécessaire de recourir à des mesures physiques pour affiner le calcul du potentiel terrestre. Les mathématiciens ont construit au dix-neuvième siècle un ensemble infini de fonctions élémentaires, appelé base des harmoniques sphériques. Cette base permet de représenter le potentiel terrestre comme une somme, a priori infinie, de fonctions proportionnelles aux harmoniques sphériques. Le problème est d’estimer les coefficients de proportionnalité, qui sont en nombre infini ! On contourne la difficulté en constatant que les mesures contiennent toujours une marge d’incertitude. Il est donc raisonnable de se limiter à un nombre fini de fonctions de base. Ce nombre peut néanmoins être très grand : des millions de coefficients sont estimés dans le modèle EGM08 utilisé actuellement.
Identification d’un ensemble de masses ponctuelles engendrant un potentiel a priori donné.
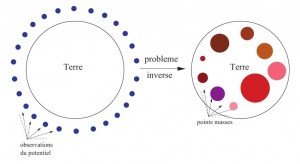
Des travaux récents visent à réduire le nombre de fonctions élémentaires, en combinant deux approximations. Une première idée est de restreindre la zone d’étude du géoïde à une partie de la Terre. Une deuxième idée est de changer la base des fonctions élémentaires, en remplaçant la Terre par un petit nombre de masses ponctuelles qui engendrent un potentiel proche de la gravité terrestre (voir figure). Une dizaine de masses sont ainsi suffisantes pour approcher, avec une précision acceptable, le potentiel terrestre à l’échelle d’un continent.
Brève rédigée par Bernard Philippe (INRIA Rennes Bretagne Atlantique).
Pour en savoir plus :
- Brève connexe : Géoïde, éllipsoïde et autres mots compliqués, par Etienne Ghys.
- Groupe de géodésie satellitaire du laboratoire dynamique terrestre et planétaire.
- Bernhard Hofmann-Wellenhof et Helmut Moritz. Physical geodesy. Springer, 2005.
- Thèse A. Abdelmoula « Résolution de problèmes inverses en géodésie physique », Co-tutelle Tunis-Rennes en cours.
- Le modèle de gravité GRACE.
Crédits Image :
Fig. 1) Photo appartenant au domaine public.
Fig. 2) Graphique de A. Abdelmoula, équipe Sage, Inria Rennes et LAMSIN, Université de Tunis.
Imprimer
1 commentaire