Prévoir le temps est particulièrement difficile lorsque la circulation atmosphérique est instable. La météo de cette année en est un parfait exemple ! Pourtant, prédire avec fiabilité l’intensité et la trajectoire d’une tempête est nécessaire tant pour des raisons humaines qu’économiques. Pour augmenter cette fiabilité, Météo France a mis en service, dans les années 2000, des méthodes mathématiques d’assimilation de données, en particulier parce que ces méthodes auraient permis de mieux prévoir la tempête de 1999.
La précision des prévisions météorologiques ne cesse d’augmenter, grâce à une puissance de calcul toujours plus importante et une compréhension plus fine des phénomènes physiques, mais également à l’aide de méthodes mathématiques. Les méthodes d’assimilation de données utilisent les observations du passé pour décrire plus précisément l’état initial de la prévision de l’atmosphère, c’est-à-dire le temps qu’il fait aujourd’hui. De ce fait, elles améliorent les prévisions.
Mais pourquoi ces méthodes utilisant des informations du passé améliorent les prévisions futures ? L’effet est dû à la part de chaos contenu dans l’évolution de l’atmosphère. L’analyse de modèles simplifiés [de Lorenz] montre qu’une petite perturbation peut entraîner en quelques jours une modification complète de l’atmosphère. Ce résultat porte un nom familier : l’effet papillon ! Il est donc crucial de bien connaître le temps d’aujourd’hui.
Schéma présentant les différentes étapes du processus d’assimilation de données
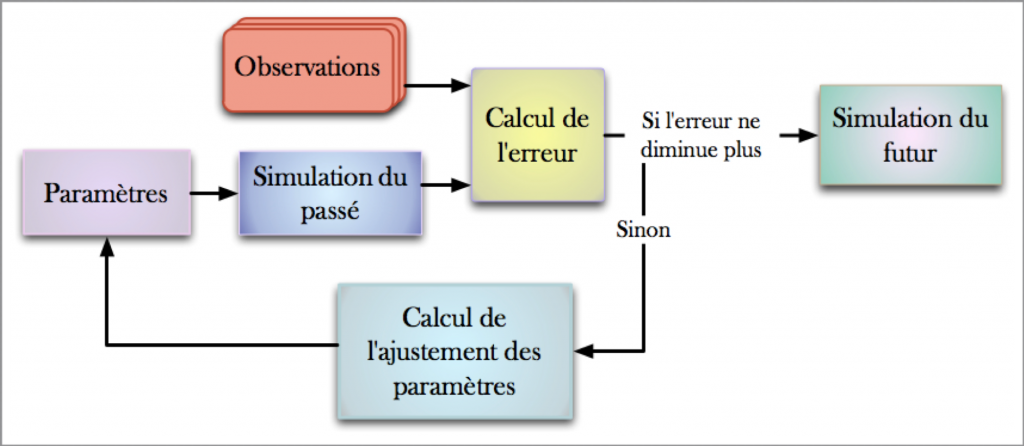
De nombreuses méthodes d’assimilation existent. Celle utilisée par Météo France, appelée la méthode variationnelle, est basée sur la théorie du contrôle optimal. Les paramètres de la simulation, connus avec imprécision (modèle trop complexe, nombre de paramètres très important), sont ajustés jusqu’à ce que la simulation prédise les événements passés ainsi que le temps d’aujourd’hui. Pour cela, nous mesurons la différence entre la valeur d’une observation (par exemple, la température donnée par une sonde) et la valeur calculée par la simulation. L’idée est que cette erreur diminue à chaque nouvel ajustement des paramètres.
En pratique, trouver les bons ajustements n’est pas chose facile. L’effet chaotique des équations implique l’existence possible de plusieurs minima locaux (le fond d’un lac de montagne est un minimum local) dans lesquels nous pouvons rester bloqués. Trouver des méthodes pour gérer ces difficultés est un sujet de recherche préoccupant.
Il n’empêche que ces méthodes, même utilisées dans une version simplifiée, peuvent assimiler efficacement 7 millions de données météorologiques par jour ! Elles sont aussi appliquées à de nombreuses autres prévisions : crues, écoulement des calottes glacières, propagation des feux, etc.
Brève rédigée par Emilie Neveu (LAMA, Université de Savoie et ARP ANR MathsInTerre).
Pour en savoir plus :
- Brève sur l’effet papillon.
- Brève connexe sur la prévision des crues.
- Sur la théorie du chaos, par Jos Leys, Étienne Ghys et Aurélien Alvarez.
- Sur la simulation des phénomènes météorologiques , un article sur Interstices.
Crédits images : Météo France, Emilie Neveu.
Imprimer
3 Commentaires