Où vont les nuages ?

Image satellite MSG canal infrarouge, système nuageux convectif.

Image satellite de densité de glace au Pôle Nord.

Pour suivre le parcours d’un nuage dans une séquence d’images, il devrait suffire d’en connaître le contour, n’est-ce pas ? Certes, mais c’est tout sauf simple !

La première difficulté relève de la nature même de l’image, qui est un objet 2D, autrement dit plan. Or, un nuage est en réalité un volume tridimensionnel, dont l’image ne nous montre qu’une vision partielle (bidimensionnelle) de son déplacement. Par exemple on verra bien le nuage se déplacer horizontalement, en revanche ses mouvements verticaux nous seront invisibles (quoique bien réels). Les images produites par les satellites manquent donc de relief mais sont également excessivement précises. Tellement précises qu’elles contiennent beaucoup de détails que même les meilleurs modèles météo ne sont pas capables de reproduire ! Nous avons donc affaire à une incohérence entre le modèle d’atmosphère et l’image.

Pour pouvoir tirer parti des images, il nous faut donc construire de nouveaux modèles plus adaptés. C’est la seconde difficulté de ce problème. Les nouveaux modèles d’évolution sont construits en ajoutant des termes aléatoires à partir d’histogrammes d’intensité lumineuse sur les images. Ces termes aléatoires ne sont pas choisis au hasard ! Ils représentent l’erreur entre le modèle et les images.

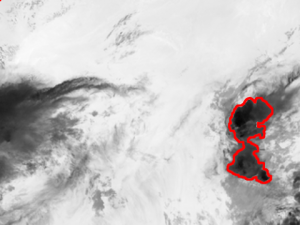
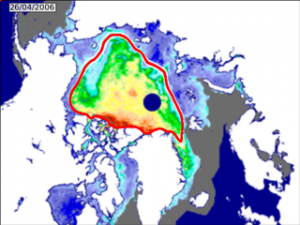
Cette technique, qui fait appel à la méthode de Monte-Carlo, a été expérimentée pour suivre dans le temps deux phénomènes différents : des systèmes nuageux à partir d’images satellites du canal infrarouge ainsi que l’évolution de la densité de glace au Pôle Nord. Notons que dans ce dernier cas, les données sont indisponibles lors des mois d’été en raison d’une couche d’eau résiduelle sur la glace, qui rend 25% des données inexploitables. Vous pouvez observer ci-dessous deux exemples de films illustrant les résultats de ce modèle. Ces modèles empiriques sont adaptés à une compréhension du passé et à des prévisions à très court terme. Ces prévisions sont essentielles pour des applications de surveillance ou de navigation aérienne. Quant à l’analyse de données passée, elle peut permettre l’extraction d’informations pertinentes pour les géophysiciens.

L’observation de données satellites de plus en plus précises propose donc un champ d’investigation immense pour les mathématiques appliquées. Ce domaine s’appuie en effet sur un paradoxe : on voit de plus en plus précisément des phénomènes dont on comprend mal toute la complexité. On pense souvent (à tort) que ce que nous percevons est immédiatement interprétable par la machine et les modèles numériques. Cela nous conduit souvent à croire (toujours à tort) que les réponses à nos questions résident uniquement dans une visualisation de plus en plus précise des phénomènes. Eh bien non ! Qu’on se le dise, les choses ne sont pas si simples ! Il y a encore bien des choses à comprendre dans le détail.

Brève rédigée par Etienne Mémin (Directeur de recherche INRIA, responsable de l’équipe FLUMINANCE). L’équipe FLUMINANCE est rattachée au centre INRIA Rennes – Bretagne Atlantique et au centre IRSTEA Rennes.