Quoi ma CFL, qu'est-ce qu'elle a ma CFL ?

Richard Courant.

Richard Courant, Kurt Friedrichs et Hans Lewy sont trois mathématiciens allemands, émigrés aux Etats-Unis dans les années 30 à cause de la montée du nazisme. En 1928, ils publient un article révolutionnaire concernant l’analyse d’équations aux dérivées partielles et leur approximation numérique. Ce travail marque encore la démarche des mathématiciens appliqués contemporains. Il met en évidence une condition nécessaire pour qu’un algorithme de calcul produise une solution cohérente, critère qu’on évoque depuis sous le nom de “condition CFL”.

Prenons par exemple l’équation des ondes. Elle décrit l’évolution d’un signal $u$ , dépendant des variables de temps $t$ et d’espace $x$ , qui se propage à vitesse $c>0$ . On sait exprimer la solution de ce problème en fonction des conditions initiales par une formule relativement simple, la formule de D’Alembert. Cette formule nous apprend notamment que la solution $u$ évaluée au point $(t,x)$ ne dépend que des valeurs prises par le signal donné à $t=0$ pour des positions dans l’intervalle $[x-ct,x+ct]$ .

Puisqu’on dispose d’une telle formule, il peut sembler de peu d’intérêt d’élaborer une méthode d’approximation numérique pour ce problème. Néanmoins, si on veut aborder des cas plus complexes (équation posée sur un domaine multidimensionnel de géométrie compliquée, vitesse de propagation variable, situations de sismologie), on devra avoir recours à une telle méthode d’approximation, et un préliminaire indispensable consiste à la valider sur ce cas simple.

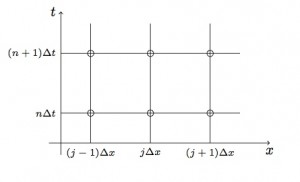
Un schéma numérique définit un algorithme, une suite d’opérations élémentaires qu’on peut confier à un ordinateur afin de calculer une approximation de la solution de l’équation. Mais l’ordinateur ne manipule que des valeurs discrètes, censées approcher la solution du problème continu sur une grille de l’espace-temps définie par des pas de temps $\Delta t>0$ et d’espace $\Delta x>0$ fixés (Fig. 1). Pour la méthode analysée par Courant, Friedrichs et Lewy, l’inconnue numérique au point $(n\Delta t, j\Delta x)$ de cette grille ne dépend que des valeurs prises par le signal initial pour une position dans l’intervalle $[(j-n)\Delta x, (j+n)\Delta x]$ . Ce domaine doit englober le vrai domaine de dépendance $[j\Delta x -cn\Delta t,j\Delta x +cn\Delta t]$ , ce qui requiert donc $c\Delta t\leq \Delta x$ .

Fig. 1 : Maillage temps-espace de pas Delta x, Delta t.

Evolution dans le temps et l'espace de la solution. La condition CFL est satisfaite ; la solution approchée n'est quasiment pas discernable de la solution exacte.

Fig. 2 : Evolution dans le temps et l’espace de la solution. La condition CFL est satisfaite ; la solution approchée n’est quasiment pas discernable de la solution exacte.

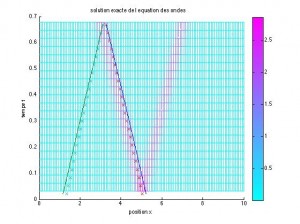
Fig. 3 : Figure 2 “vue de dessus”. La zone entre les traits pleins représente le vrai domaine de dépendance pour le point x=3.5, t=0.7, celle entre les croix le domaine de dépendance numérique.

Les figures montrent ce qui se passe lorsque cette condition est satisfaite (Fig. 2-3) ou non (Fig. 4). Si on veut augmenter la résolution spatiale (diminuer $\Delta x$ ), il faut aussi réduire le pas de temps $\Delta t$ … et donc augmenter le temps de calcul pour mener la simulation jusqu’à un même temps final fixé, et la contrainte est d’autant plus sévère que la vitesse de propagation $c$ est grande. Cette contrainte est directement liée au fait que l’équation décrit un phénomène de propagation à vitesse finie. Elle exprime un critère de stabilité.

L’analyse de ces contraintes pour des schémas et des problèmes plus complexes, par exemple en mécanique des fluides, est un enjeu capital du calcul scientifique, qui réclame des outils sophistiqués et une profonde compréhension du problème physique sous-jacent.