Des poires en rotation !

Imaginez une planète liquide dans l’espace, très éloignée de tous les autres objets célestes. Imaginez encore que cette masse est immobile, en équilibre parfait. Que signifie un tel équilibre ? Une petite goutte de liquide à la surface est attirée par toutes les autres gouttes de la planète sous l’influence de forces gravitationnelles.

Si la force totale qui en résulte n’était pas perpendiculaire à la surface, pointant vers l’intérieur de la planète, la petite goutte aurait tendance à se déplacer et la planète ne serait pas en équilibre. C’est le fait que le fil à plomb est perpendiculaire au niveau des mers qui caractérise l’équilibre.

Quelles sont les formes d’équilibre possibles ?

Une sphère est une solution car, à cause de sa symétrie parfaite, la force d’attraction qui agit sur n’importe quel point de la surface doit être dirigée vers le centre de la sphère, donc perpendiculairement à la surface. Y a-t-il d’autres solutions ?

Pendant longtemps, il est apparu comme une évidence que la seule forme possible pour une planète liquide immobile soit celle d’une sphère. Le mathématicien allemand Lichtenstein en a apporté la preuve en 1918. Le rôle du mathématicien serait donc de démontrer, avec beaucoup de retard, ce que tous les physiciens savent depuis bien longtemps ? Quel est l’intérêt d’un tel théorème, dont la preuve n’est pas évidente, mais qui ne surprend personne ?

Eh bien, c’est que, parfois, il y a des surprises ! Considérez maintenant une planète qui n’est plus immobile mais qui tourne autour d’un axe, avec une vitesse constante. A la force d’attraction gravitationnelle, il faut maintenant ajouter une force centrifuge et c’est la somme de ces deux forces qui doit être perpendiculaire à la surface. En 1741, le mathématicien écossais Maclaurin trouve une solution : il montre que l’ellipsoïde homogène de révolution peut aussi être figure d’équilibre.

De façon générale, peut-on affirmer que la forme de la planète en équilibre doit être ce qu’on appelle une surface de révolution, c’est-à-dire invariante par les rotations autour de l’axe ? Là encore, « tout le monde » pensait que c’était évident :  puisque le problème est invariant par les rotations, la solution « doit » l’être également. Et pourtant… ce n’est pas exact. En 1834, le mathématicien Jacobi montre que si on fait tourner un ellipsoïde asymétrique (voir la figure) autour d’un axe bien choisi, avec une vitesse bien calculée, la « planète » est en équilibre. Un problème symétrique qui a une solution asymétrique… Bizarre ? C’était une surprise à l’époque, mais aujourd’hui c’est une « évidence » : on parle de brisure de symétrie.

Le lecteur pensera peut-être que la Terre est solide et non liquide ! Et pourtant, pour un géophysicien, la Terre est solide et fluide... C’est un peu comme un glacier : si vous en prenez une photo tous les ans et que vous faites passer ensuite un film à raison de 25 images par seconde, vous verrez un fleuve qui coule… donc fluide.

Pour la Terre, c’est la même chose : à des échelles de temps très grandes, on peut la considérer comme un objet fluide.

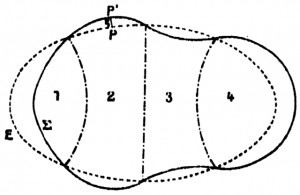
Il n’empêche que le problème simple de l’équilibre des masses fluides et homogènes en rotation a été pendant quatre siècles un moteur puissant de la science. Les plus grands scientifiques ont essayé de déterminer théoriquement l’ensemble des formes d’équilibre possibles : Clairaut, D’Alembert, Laplace, Lagrange, Legendre, Liouville, Dedekind, Dirichlet, Riemann, Lyapounov, Poincaré, Cartan, Appell, Chandrasekhar, etc. Fin XIXème, une véritable école française se forme même autour du sujet : Hamy montre que les résultats précédents ne peuvent être généralisés aux ellipsoïdes hétérogènes et Radau trouve une simplification étonnante et très ingénieuse à l’équation de Clairaut, tandis que Poincaré montre l’existence de formes plus étranges, qu’il qualifie de piriformes : des poires en équilibre (voir la figure) !

Cette question a engendré un grand nombre d’idées fondamentales, et utiles,  en mathématiques mais aussi en physique. Malgré tout, il reste au moins autant de questions que de réponses. Y’a-t-il d’autres figures possibles ?  Nous n’en savons rien. Encore mieux, si l’on peut dire : on ne sait pas résoudre mathématiquement la forme d’équilibre d’un fluide hétérogène (on ne connaît que la solution approximative de Clairaut) ! Ce champ de recherche qui a passionné des générations de mathématiciens est tombé en désuétude.