Des triangles pour se repérer sur Terre

Gemma Frisius, peint par Maarten van Heemskerck.

Qui connaît le nom de Gemma Frisius (1508-1555), professeur néerlandais de mathématiques ? Et pourtant son traité Libellus de Locorum describendorum ratione (1533) a une influence considérable sur nos connaissances scientifiques. Il contient en effet le plus ancien exposé connu du principe de triangulation.

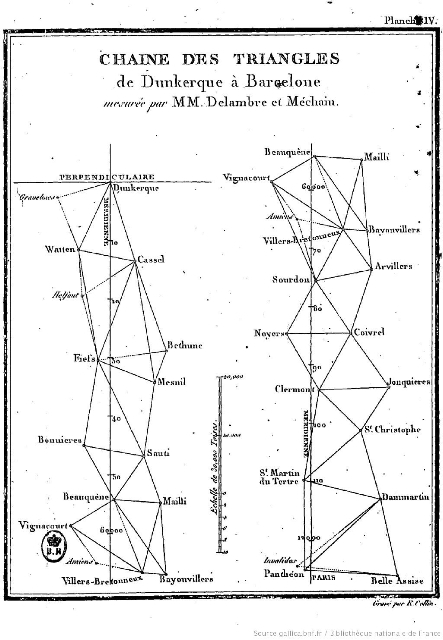
Cette méthode repose sur une idée simple mais extrêmement fertile : il est beaucoup plus facile de mesurer des angles que des distances. Pour déterminer la géométrie d’un territoire, on commence par découper celui-ci en triangles de façon à ce que depuis les sommets, choisis en hauteur, on puisse voir d’autres sommets (en terrain plat on se met en recherche de clochers ou de tours de châteaux bien placés). Depuis chaque sommet, on mesure l’angle entre les directions de visée vers deux autres sommets. Prenons par exemple la mesure réalisée par Delambre et Méchain pour la méridienne de France entre Dunkerque et Barcelone (cf. image ci-dessous).

La triangulation de la méridienne de Paris, par Delambre et Méchain.

Depuis Dunkerque, on commence par mesurer l’angle entre les directions de Watten et Cassel. Le principe est relativement facile : on pose un cercle gradué horizontalement. En son centre, on pose un axe sur lequel tourne une lunette mobile horizontale (dans la pratique l’instrument utilisé s’appelle théodolite et la lunette tourne aussi dans le plan vertical). On vise le premier sommet, on note l’angle que fait la lunette avec le zéro du cercle, puis on recommence avec l’autre sommet. La différence des deux angles donne l’angle au sommet-Dunkerque. Avouez que cette mesure est beaucoup plus facile à réaliser que celle de la distance sur le terrain entre Watten et Cassel pour laquelle il faudrait marcher d’une ville à l’autre en ligne droite tout en transportant son décamètre de proche en proche.

Sur l’ensemble de tous les triangles, il faut tout de même mesurer un côté d’un triangle ; on appelle cela la base. En effet, un triangle est entièrement déterminé par deux angles et une base. De proche en proche, la trigonométrie permet alors de résoudre toutes les distances du pavage et donc la distance de Dunkerque à Barcelone.

La triangulation, cette science très ancienne, est tellement utile qu’elle est restée une méthode fondamentale de géodésie, c’est-à-dire de positionnement à la surface de la Terre. Elle a même été décisive pour Newton dans sa découverte de la gravitation universelle. Comment ? Ce sera l’objet d’une autre brève.

Brève rédigée par, Frédéric Chambat (École Normale Supérieure de Lyon) et Étienne Ghys (CNRS et École Normale Supérieure de Lyon).

Brèves connexes :

• La mesure de la Terre – Gauss et la théorie des surfaces sur Mathématiques pour la planète Terre 2013.
• Géoïde, ellipsoïde et autres mots compliqués sur Mathématiques pour la planète Terre 2013.

Pour en savoir plus :

• Géométrie, mesurer la terre, mesurer la Terre ?, Michèle Audin sur l’Images des mathématiques.
• Ouvrage de référence, « La figure de la Terre, du XVIIIe siècle à l’ère spatiale », sous la direction de Henri Lacombe et Pierre Costabel, Académie des Sciences, Gauthier-Villars 1988.
• Triangulations : de la terre au nœud de trèfle, Julien Marché sur l’Images des mathématiques.

Crédits images : Wikimedia commons et BNF-Gallica.

Imprimer