Tsunami : reconstruire la vague

Le tsunami du 26 décembre 2004 a été l’un des plus meurtriers de tous les temps.

Un tsunami est une onde marine exceptionnelle qui, en s’approchant des côtes, s’exprime par des vagues de très haute énergie et une inondation des zones côtières. Le terme est dérivé d’un mot japonais qui signifie « vague portuaire ».

Le tsunami du 26 décembre 2004 a touché une dizaine de pays dont certains situés à plusieurs milliers de kilomètres de l’épicentre du séisme. Il a causé la mort de plus de 280 000 personnes. C’est le tsunami le plus dévastateur et l’une des catastrophes les plus meurtrières de tous les temps. L’Indonésie a été le pays le plus affecté.

Si les vagues du tsunami se brisent habituellement en mer ou sur la ligne de côte, la vague principale du tsunami de 2004 s’est brisée en arrière de la plage, ce qui lui a conféré la capacité d’avancer profondément dans les terres. La plus haute vague atteignit environ 17 m et diminua de 20 à 60 cm de hauteur par 100 m parcourus.

Pour établir des stratégies de prévention efficaces, il est important de pouvoir reconstituer le trajet de la vague, or les modèles d’hydro-dynamique ont été principalement étudiés sur la mer et reflètent mal le comportement de la vague sur terre.

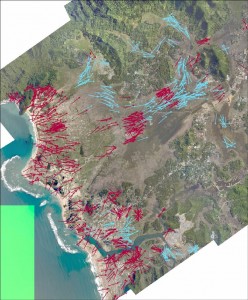
Dans le cadre du programme de recherche international Tsunarisque, environ 1000 angles formés par l’orientation des objets cassés ou arrachés par la vague lors de son passage (arbres, poteaux, etc.) sur une zone de 20km² ont été relevés. Les orientations mesurées sont la trace de la dernière vague passée à l’emplacement du relevé. Les angles relevés ne couvraient néanmoins pas toute la zone d’étude et pour reconstituer le trajet de la vague, il a fallu les interpoler.

L’orientation des objets tombés après le passage de la vague permet de reconstituer son trajet.

Le principe de l’interpolation spatiale (krigeage) est d’estimer les données en chaque point comme une moyenne pondérée des données observées en différents points de l’espace. Cependant la moyenne arithmétique ne peut être utilisée pour des données circulaires (la moyenne d’un angle de 10 degrés et d’un angle de 350 degrés n’est évidemment pas un angle de 180 degrés). De plus, la moyenne d’angle n’est pas invariante par rotation, c’est-à-dire que la moyenne des angles par rapport au Nord n’est pas égale à la moyenne des angles par rapport au Sud. Ce problème est aussi rencontré dans d’autres situations, par exemple l’estimation de la direction (et la force) du vent dans différents endroits, comme un aéroport, une grue, ou autre.
En utilisant les propriétés des nombres complexes, une méthode statistique d’interpolation spatiale d’angle, invariante par rotation, a permis de reconstituer la trajectoire du tsunami là où les témoignages étaient rares. Cela a permis d’améliorer la connaissance sur ce phénomène et donc d’améliorer les procédures d’alerte auprès de la population en précisant par exemple la taille de la zone à évacuer.

Brève rédigée par Avner Bar-Hen (Université Paris Descartes) et Delphine Grancher (CNRS) d’après leurs travaux.

Pour en savoir plus :

Grancher, D., Bar-Hen, A., Paris, R., Lavigne, F., Brunstein, D., Wassmer, P. , (2011), Interpolation spatiale de données circulaires : application au tsunami du 26 décembre 2004. , In : Lavigne F. & Paris R. (eds). Tsunarisque : le tsunami du 26 décembre 2004 à Aceh, Indonésie. Publications de la Sorbonne, Paris , 49-58.
Site du projet Tsunarisque.
Frédéric Dias, «Tsunamis, vagues scélérates et leur modélisation», Interstices, INRIA, 2007.
Frédéric Dias, « Modélisation mathématique des tsunamis », Images des Mathématiques, CNRS, 2011.
Brèves connexes : « Des équations pour les vagues » et « Des vagues hors du commun ».